Utilização de modelos computacionais na construção da prova matemática

Tese submetida à Faculdade de Ciências da Universidade do Porto
para a obtenção do grau de Mestre em Ensino da Matemática

Resumo

Este trabalho propõe uma possível abordagem à utilização de modelos computacionais como ferramentas de ensino, auxiliares na construção (no sentido da génese) da prova matemática, incluindo a construção – interiorizada – do sentimento da própria necessidade da prova. Foram elaboradas duas tarefas de modelação baseadas em provas conhecidas de dois resultados de natureza matemática distinta e cuja aplicação se destina, à partida, a diferentes níveis de escolaridade. Na modelação das provas foram utilizados dois programas, o Mathematica e o LiveGraphics3D , através dos quais foi possível munir os modelos computacionais com funcionalidades específicas, adaptadas às características da estrutura de ambas as provas.

1. O Teorema de Dandelin

Introdução

Modelo

A primeira tarefa de investigação explora a demonstração do teorema de Dandelin. A escolha deste tema deveu-se à possibilidade de, através de modelos computacionais adequados, ser possível adaptar um resultado complexo sobre cónicas a uma tarefa de investigação possível de realizar ao nível do ensino secundário.
Dandelin apresentou, em 1822, uma demonstração curiosa para a propriedade focal da elipse, como consequência da sua definição enquanto secção de um cone. Para tal, utilizou duas esferas na sua demonstração, que ficaram conhecidas como as esferas de Dandelin. A originalidade da prova que apresentou para este resultado está precisamente na utilização de dois objectos que, embora estranhos ao enunciado do resultado, têm um papel fundamental e mesmo facilitador no desenrolar da prova.

2. O modelo hiperbólico e o modelo de Poincaré

Introdução

Modelo

A segunda tarefa de investigação pode ser utilizada na comparação de dois modelos euclideanos do plano hiperbólico: o modelo hiperbólico e o modelo de Poincaré . Baseou-se no seguinte teorema:

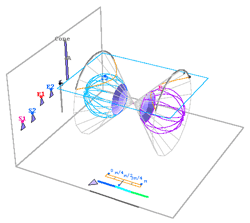
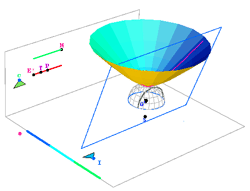
Seja H um hiperbolóide de equação 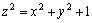e C o círculo de raio um, centrado na origem e contido no plano 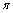de equação 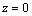. Seja 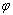a projecção estereográfica de centro 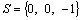que a cada ponto 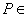H faz corresponder um ponto tal que .

Então:

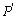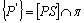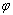1. A restrição de a H é uma bijecção sobre o interior de C .

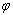2. A imagem por da intersecção de H com um plano que passa pela origem é a parte interior a C de uma circunferência que lhe é ortogonal ou é uma recta que passa pela origem.

Os modelos elaborados centram-se na demonstração do segundo ponto deste teorema.